天文攝影的信噪比: 決定圖像品質的基石
oldmiow
天文攝影的信噪比 :
決定圖像品質的基石
上手天文攝影預處理與疊合 : Siril操作示範 彩色篇 文中一大重點便是"疊合" (stacking),有些文章稱"疊加"(通常不是加法),另有稱"積分" (integration),總而言之就是拍攝多張影像,將多張影像透過平均值 (或其他方式,比如中位數) 結合成一張影像,這麼做的目的是為了提升信噪比,也就是信號 (訊號) 對噪的比值,不為過地說,足夠高的信噪比是好天文攝影作品的一大基石。
信噪比的效應
 |
| (圖一),IC342 "隱藏的星系" 這個星系的視大小將近三分之二個滿月大, 但是由於視方向上靠近銀河盤面, 受到銀河系塵埃的消光影響,亮度相比 M101 (風車星系)、M51 (螺旋星系) 更暗,更難拍攝,也因此更冷門, 較少人拍攝這個目標,筆者在2019年11月底 前往合歡山時便選擇拍攝這個目標, 這也是筆者第一個拍攝總曝光時間 超過五個小時的天體,總曝光時間6小時9分鐘。 |
(圖一) 為筆者所拍攝並處理的IC342星系,雖然影像沒有達到非常高的信噪比,但是信噪比已足夠顯現出許多不同的結構比如星系的螺旋,且畫面也相對滑順,沒有太明顯花花綠綠顆粒感的情況。
如果信噪比太低,影像則會有很重的顆粒感,顯得花花綠綠的,如下方 (圖二) ,注意圖中比較亮的區域相對於較暗的區域,沒有那麼嚴重的花花綠綠感,這引出了個重要概念 - 同一張影像上亮度不同的部分信噪比不一樣,亮部信噪比較好。
 |
| (圖二),M42 獵戶座大星雲 上手天文攝影預處理與疊合 : Siril操作示範 彩色篇 文章一開始那幅M42作品 (見下圖) 的 曝光30秒單張原始素材裁切局部,經過去拜爾、 轉色、非線性處理,用以展示低信噪比。 |
 |
| (圖三),M42 獵戶座大星雲 完整介紹見 上手天文攝影預處理與疊合 : Siril操作示範 彩色篇 原始素材由 Aaron Chen 提供 疊合了72張(圖二)30秒曝光的影像, 經過預處理、疊合、後處理完的成品, 圖像明顯顆粒感減少,更滑順了, 顏色差異來自校準跟調色,此外 (圖二) 的 低信噪比會影響校準的準確定,也更難 調出多采多姿的顏色,容易偏向某一色調 |
下方的 (圖四) 用GIF動圖展現隨著疊合的張數越來越多、總曝光時間越來越長,從而信號累積越來越多,影像逐漸從顆粒感十足變得越來越滑順,在只有1張的時候整張影像顆粒感都很重,疊合數量到16張的時候星系核心附近已經滑順不少,但是外圍較暗區域顆粒感還是很重,再到疊合63張之後整體又滑順了些,雖然外圍區域還是有些顆粒感,但遠比只有1張的時候滑順。
 |
| (圖四),GIF動圖,IC342星系部分局部放大 來自於 (圖一) 的原始影像,單張影像為 L濾鏡 (通過幾乎整段可見光) 下曝光3分鐘, 圖像左上角的數字表示疊合張數,因此 x1表示單張曝光,總曝光3分鐘 x2表示2張疊合,總曝光6分鐘 x4表示4張疊合,總曝光12分鐘 x63表示63張疊合,總曝光189分鐘 不同張數疊合的影像大致拉伸到相近的明暗對比程度 |
 |
| (圖五),從 (圖四) 中挑出的x1、x4、x16、x63 以靜態圖供讀者更仔細檢視影像各部位的變化 |
泊松分佈
看完信噪比的效應後,接著是時候了解信噪比的基本概念了,這部分應用一點簡單的數學粗略介紹幾個統計學概念。
天文攝影在捕捉宇宙中各式天體所發出的光子,信噪比中的信號便是這些光子,而這些光子有個特殊的性質 - 泊松分佈 (Poisson distribution)。
泊松分佈是一種不連續的分佈,對於光子這樣一顆一顆的粒子,在單位時間內抵達我們感光元件的光子,有時候多而有時候少,但是隨著採集到的光子越來越多,單位時間抵達的光子平均起來,會逼近真正的值,換言之,天文攝影增加總曝光時間做的,就是在累積越來越多的光子信號。
泊松分佈的 期望值 (expected value,平均值 mean) = 變異數 (variance, 或譯方差)
μ = Var(x)
變異數 (variance, 或譯方差) 開平方根就是 標準差(standard deviation) ,也就是說
μ = Var(x) = σ²
μ = Var(x) = σ² 是非常特別的,不是所有事件都有這種特徵,以下舉例個不是泊松分佈的信號,也讓讀者了解幾個統計學名詞的含意
1. 期望值 (expected value,符號 μ): 在此處可以理解成平均值(mean),將所有不連續的統計值加總起來除以統計次數,比方我們對某實驗統計5次信號,5次統計到的信號強度x是 10、13、12、8、15
期望值 = 信號總強度 ÷ 統計次數
μ = (10+13+12+8+15) ÷ 5
μ = 11.6
2. 變異數 (variance, 或譯 方差,符號 Var(x)): 在此處含意是每一次統計,距離平均值(mean)的差距平方之後全部加起來,除以統計次數 (拍攝張數 n)
Var(x) = Σ(x-μ)² ÷ n
= [(10-11.6)² + (13-11.6)² + (12-11.6)²
+ (8-11.6)² + (15-11.6)²] ÷ 5
= [2.56+1.96+0.16+12.96+11.56] ÷ 5
變異數 Var(x) = 5.84
期望值(平均值) μ = 11.6
很顯然,變異數不等於期望值,這個實驗的統計值不是泊松分佈! 但星光、宇宙天體來的光子,卻十分有趣地呈泊松分佈。
信噪比的涵義
上一段提到泊松分佈的重要性質 μ = Var(x) = σ² (平均值 = 變異數 = 標準差的平方),而天文攝影的光子信號便為泊松分佈,其中標準差σ表示信號的離散程度,我們可以大致理解成不確定程度,標準差σ越大,這個信號的不確定程度就越大,也就是偏離真正值的漲落(多或少)這個不確定程度更大,而μ = σ²,因此
實務上,平均數μ在天文攝影中可由我們拍攝的信號量近似來代表,天體的光子在半導體感光元件上激發產生S個電子的信號儲存下來,信號S的不確定程度σ就是S開平方根,而信號的不確定程度σ其實就是信噪比中的"噪" N,因此
不確定程度 = 信號開平方根 = 噪
如此我們終於得到了信噪比(SNR, signal to noise ratio)的表達
上面的涵義便是,對單一信號而言,它的噪就是本身信號的不確定程度,這是泊松分佈信號的內在性質。
信號不只來自我們想要拍攝的天體,也有我們不要的信號,比如光害、暗電流等等,這些信號都會有連帶的不確定程度,此外還有電子信號從半導體元件讀出的不確定程度,這些不確定程度的加總方式和誤差傳遞計算一樣,採用平方相加之後開根號,因此最終我們得到了如下表示
 |
| (相對完整的信噪比表達式) |
S: 信號
N: 噪,不確定的程度
S obj.: 來自天體的信號
S sky: 來自天光的信號,天光是氣輝、各式光源在大氣中散射的光害、宇宙雜散的光子等等綜合起來的效應
D: 暗電流信號,在固定溫度下隨時間線性累積的信號,由於暗電流是信號,所以它的不確定程度就是其開平方根,且由於是信號,所以可以扣掉,在預處理中扣暗場的目的便是這,但是信號可以扣掉,信號的不確定程度卻會留下來
R: 讀出噪,這一項是噪,因此有個平方。 讀出噪包含讀出過程的不確定程度,簡單舉例來說 一個信號應該是100,但是讀出的時候有時候讀成99,有時候讀成103,有時候讀成98,又有時讀成105,當讀出很多次的值平均起來,會逼近應該要有的值100。讀出噪可能但不一定是高斯分佈,不過為了方便估計,我們把它當作泊松分佈計算
在天文研究中,信噪比(SNR)大約3~5可以認為我們偵測到了某個天體,而SNR到了10左右可以做比較粗糙的測光(photometry),對SNR約100的目標測光就能取得相對誤差1%的高品質亮度信息。
而對天文攝影而言,通常需要更高的信噪比,這是由於要做劇烈的暗部擴張,將細微的亮暗差別給擴大,至於實際需要多少則依不同處理有不同要求。此外如前面所言,天體不同部分的亮度不同,比如星系核球附近的表面亮度可能就是外圍旋臂的好幾倍到幾十倍,而其他空曠的天區在深度曝光後可能可以顯露出星際的塵埃帶,這些塵埃帶的亮度又暗得多,因此天文攝影中,亮部信噪比足夠但暗部信噪比依然不足是常有的現象。
噪和雜訊的真正涵義
雜訊和噪常常被混為一談,其實包含了 "我們不要的信號 (雜訊) " 跟 "不確定程度 (噪) " 兩個部分,兩部分並不相同,有一些領域將之混為一談,但是在天文攝影中需要分開討論。不要的信號 (雜訊) 如光害、暗電流、固定噪等等皆是信號,信號是可以扣掉的,影像如果有很強的光害但沒有過曝,是可以扣掉光害信號額外添加在整張影像上的值,但是很強的光害信號所連帶 "很大的不確定程度" 卻扣不掉,最後影像上不同像素間有了很大的不確定程度造成的漲落差異,兩個原本應該亮度一樣的區域,因為漲落而有了很大的亮暗變化,就形成了很重的顆粒感。
以下 (圖六) 以及 (圖七) 是透過單色感光元件搭配濾鏡連續拍攝的數張影像,每一張影像的曝光時間皆相同,影像皆已使用暗場、偏壓場以及平場校正過,並且將座標對齊,可以明顯看出影像上同樣的區域,像素的強度值皆不相同,而呈現漲落、變動的狀態,這個 "噪" 越大,就表示這種漲落的程度越大。
 | |
| 圖六,5張連續曝光的目標, 每一張皆採用完全一樣的曝光時間 下方的 (圖七) 為本圖的gif版 |
 |
| 圖七, (圖六) 的gif動圖 |
看完了單色影像下的 "噪" ,接下來看回 (圖二,見下方) 彩色影像,在單色灰階影像中,漲落只能體現在強度 (亮暗) 上,而本質上,彩色影像就是數張單色灰階影像組成,下圖就是紅、藍、綠三色合成的彩色影像,因此影像上一片原本應該色調均勻且滑順的區域,會因為三色各自的漲落,導致有的像素紅色強,有的像素綠色強,有的像素則是藍色強,從而形成花花綠綠的樣貌。
 | |
| (圖二),M42 獵戶座大星雲, 較暗的區域中,花花綠綠的很明顯 |
總和上文說明的內容,噪的真正含意,便是不確定漲落的程度,而造成這種不確定漲落的原因,則來自於隨機的過程,比方
1. 光子的自然隨機特性
2. 暗電流電子的隨機特性
3. 其他添加的信號比如輝光,也展現了隨機特性
4. 感光元件信號在讀出過程中的隨機特性
其中 1. 和 2. 以及 3. 可以直接透過測量影像上的像素強度,換算成信號電子量,再將信號開平方根得到噪的強度;而 4. 則可以透過泊松噪的統計學特徵,從圖像直接計算出噪的強度 (讀出噪)
由於噪是自然的隨機過程所造成的漲落,因此無法如 "將一張影像減去另一張影像" 這般 "扣" 掉噪,這種扣法就算可以扣掉暗電流等等不要的信號,也無法扣掉其噪,唯一能夠對付噪的做法是累積更多天體的信號,雖然其他不要的信號也會一併累積,不過根據信噪比的公式,可以發現整個信噪比的大小是上升的,其效應就如 (圖四) (圖五) 展現的,隨著曝光的總時間越來越多,影像變得越來越滑順。
校準場的信噪比
由於噪根本無法「扣」掉,因此校準場的目的,在於移除干擾純粹天體影像的因素,比如暗電流、額外添加的偏壓、感光不均勻或者光學系統上的漸暈、灰塵陰影、像素感光性能差異,在 深入了解天文攝影預處理 : 暗場、平場、偏置場的涵義與拍攝 文中所處理的三場,其操作的都是信號,也因此三場各自也有自身的信噪比,透過拍攝多張影像提升其各自的信噪比,才能確保減法扣偏置電壓及暗電流時扣得精準;乘除平場時,乘除的比例是精準。


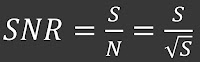
留言
張貼留言